Following a recent post, I enjoyed revisiting Brent Yorgey’s Factorization Diagrams (by the way, this in-browser animation is pretty great, too.)

I immediately wanted to try some variations, and didn’t really feel like figuring out how to compile Yorgey’s Haskell, let alone how to do something interactive with it. And then I had the thought that this might be a nice way to experiment with SwiftUI: it’s graphical, declarative, and simple enough for a novice like me (or so I hoped).

After stumbling around in a Playground for while, here’s what I came up with:

VStack {
    layout(n: 3) {
    layout(n: 2) {
        Circle().foregroundColor(.blue)
    }}
}

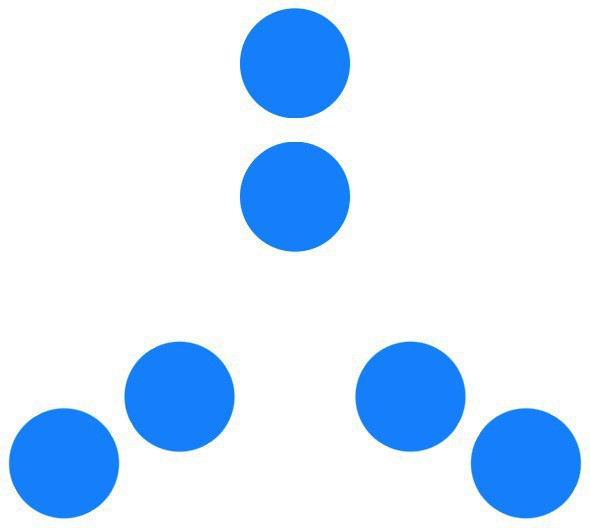
That is, draw 3 sets of 2 blue circles each, visualizing the prime factorization: 6 = 2·3 (see the first image.)

layout just applies some rotation, scaling, and offsets to n copies of its argument:

// Two fairly arbitrary parameters:
let RADIUS: CGFloat = 100
func scale(_ n: Int) -> CGFloat {
    return 1/CGFloat(n)
}

func layout<V:View>(n: Int, d: @escaping () -> V) -> some View {
    func position(i: Int) -> some View {
        let t = Angle.degrees(Double(i)*360/Double(n))
        return d()
            .rotationEffect(t)
            .scaleEffect(scale(n))
            .offset(x: RADIUS*CGFloat(sin(t.radians)),
                    y: RADIUS*CGFloat(-cos(t.radians)))
    }

    return ZStack {
        ForEach(0..<n, content: position)
    }
}

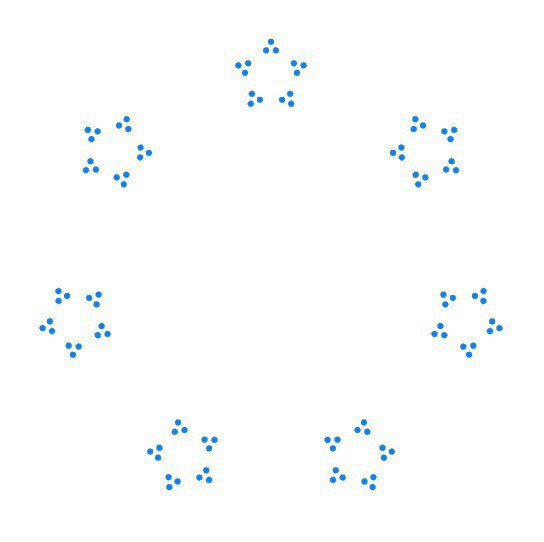
Additional nested calls produce more interesting designs (the second image):

layout(n: 7) {
layout(n: 5) {
layout(n: 3) {
    Circle().foregroundColor(.blue)
}}}

I’m pretty happy with this as far as it goes, but so far I haven’t been able to get the fancy SwiftUI types to understand an unfolded version so I could make a single call like layoutFactors([5, 3, 2, 2]) or layoutPrimeFactors(60).

6105